Use Tikhonov Regularization to Solve Fredholm Integral Equation

Background #

Fredholm integral equation of the first kind is written as,

$f(x)=\int_{a}^{b}K(x,s)p(s)\mathrm{d}s.$

The problem is to find $p(s)$, given that $f(x)$ and $K(x,s)$ are known. This equation occurs quite often in many different areas.

Discretization-based Method #

Here we describe a discretization-based method to solve the Fredholm integral equation. The integral equation is approximately replaced by a Riemann summation over grids,

$f(x_i)=\sum_j \Delta_s K(x_i, s_j) p(s_j)$

where $\Delta_s$ is the grid size along the dimension $s$ and $x_i$, $s_j$ are the grid points with $i$ and $j$ indicating their indices. When grid size $\Delta_s\to0$, the summation converges to the true integral. It is more convenient to write it in the matrix form,

$\boldsymbol{f} = \boldsymbol{\Delta}_s \boldsymbol{K} \boldsymbol{p}$

where

$\boldsymbol{f}=(f(x_1), f(x_2),\cdots,f(x_n))^{\mathrm{T}},$

$\boldsymbol{K}= \begin{pmatrix} K(x_1,s_1) & K(x_1,s_2) & \cdots & K(x_1,s_m) \\ K(x_2,s_1) & K(x_2,s_2) & \cdots & K(x_2,s_m) \\ \vdots & \vdots & \ddots & \vdots \\ K(x_n,s_1) & K(x_n,s_2) & \cdots & K(x_n,s_m) \end{pmatrix}$

$\boldsymbol{p} = (p(s_1),p(s_2),\cdots,p(s_m))^{\mathrm{T}}$

and $\boldsymbol{\Delta}_s = \Delta_s \boldsymbol{I}$ with $\boldsymbol{I}$ being the identity matrix of dimension $n \times n$.

Now solving the Fredholm integral equation is equivalent to solving a system of linear equations. The standard approach ordinary least squares linear regression, which is to find the vector $\boldsymbol{p}$ minimizing the norm $\vert\vert \boldsymbol{\Delta}_s \boldsymbol{K} \boldsymbol{p}-\boldsymbol{f}\vert\vert_2^2$. In principle, the Fredholm integral equation may have non-unique solutions, thus the corresponding linear equations are also ill-posed. The most commonly used method for ill-posed problem is Tikhonov regularization which is to minimize

$\vert\vert\boldsymbol{\Delta}_s \boldsymbol{K} \boldsymbol{p}-\boldsymbol{f}\vert\vert_2^2+\alpha^2\vert\vert\boldsymbol{p}\vert\vert_2^2$

Note that this is actually a subset of Tikhonov regularization (also called Ridge regularization) with $\alpha$ being a parameter.

When $p(s)$ is a probability density function #

In many cases, both $f(x)$ and $g(s)$ are probability density function (PDF), and $K(x,s)$ is a conditional PDF, equivalent to $K(x\vert s)$. Thus, there are two constraints on the solution $p(s)$, that is $p(s)\geq 0$ and $\int p(s)\mathrm{d}s = 1$. These two constraints translate to $p(s_i)\geq 0$ for any $s_i$ and $\Delta_s\sum_i p(s_i)=1$. Hence, we need to solve the Tikhonov regularization problem subject to these two constraints.

In the following, I will show how to solve the Tikhonov regularization problem with both equality and inequality constraints. First, I will show that the Tikhonov regularization problem with non-negative constraint can be easily translated to a regular non-negative least square problem (NNLS) which can be solved using active set algorithm.

Let us construct the matrix,

$\boldsymbol{A}= \begin{pmatrix} \Delta_s \boldsymbol{K} \\ \alpha \boldsymbol{I} \end{pmatrix}$

and the vector,

$\boldsymbol{b}= \begin{pmatrix} \boldsymbol{f}\\ \boldsymbol{0} \end{pmatrix}$

where $\boldsymbol{I}$ is the $m\times m$ identity matrix and $\boldsymbol{0}$ is the zero vector of size $m$. It is easy to show that the Tikhonov regularization problem $\mathrm{min}(\vert\vert\boldsymbol{\Delta}_{s} \boldsymbol{K} \boldsymbol{p} - \boldsymbol{f}\vert\vert_{2}^{2}+\alpha^2\vert\vert\boldsymbol{p}\vert\vert_{2}^{2})$ subject to $\boldsymbol{p}\geq 0$ is equivalent to the regular NNLS problem,

$\mathrm{min}(\vert\vert\boldsymbol{A}\boldsymbol{p}-\boldsymbol{b}\vert\vert_2^2),\mathrm{\ subject\ to\ }\boldsymbol{p}\geq 0$

Now we add the equality constraint, $\Delta_s\sum_i p(s_i)=1$ or $\boldsymbol{1}\boldsymbol{p}=1/\Delta_s$ written in matrix form. My implementation of solving such problem follows the algorithm described in Haskell and Hanson ^[1]. According to their method, the problem becomes another NNLS problem,

$\mathrm{min}(\vert\vert\boldsymbol{1}\boldsymbol{p}-1/\Delta_s\vert\vert_2^2+\epsilon^2\vert\vert\boldsymbol{A}\boldsymbol{p}-\boldsymbol{b}\vert\vert_2^2),\mathrm{\ subject\ to\ }\boldsymbol{p}\geq 0$

The solution to the above equation converges to the true solution when $\epsilon\to0^+$. Now I have described the algorithm to solve the Fredholm equation of the first kind when $p(s)$ is a probability density function. I call the algorithm described above as non-negative Tikhonov regularization with equality constraint (NNETR).

Code #

Here I show the core code of the algorithm described above.

# core algorithm of non-negative equality Tikhonov regularization (NNETR)
def NNETR(K, f, Delta, epsilon, alpha):
    # the first step
    A_nn = np.vstack((K, alpha * np.identity(K.shape[1])))
    b_nn = np.hstack((f, np.zeros(K.shape[1])))

    # the second step
    A_nne = np.vstack((epsilon * A_nn, np.full(A_nn.shape[1], 1.0)))
    b_nne = np.hstack((epsilon * b_nn, 1.0))

    # Use NNLS solver provided by scipy
    sol, residue = scipy.optimize.nnls(A_nne, b_nne)

    # solution should be divided by Delta (grid size)
    sol = sol/Delta
    return sol, residue

Examples #

• Compounding an exponential distribution with its rate parameter distributed according to a gamma distribution yields a Lomax distribution $f(x)=a(x+1)^{-(a+1)}$, supported on $(0,\infty)$, with $a>0$. $k(x,\theta)=\theta e^{-\theta x}$ is an exponential density and $p(\theta) = \Gamma(a)^{-1}\theta^{a-1}e^{-\theta}$ is a gamma density.

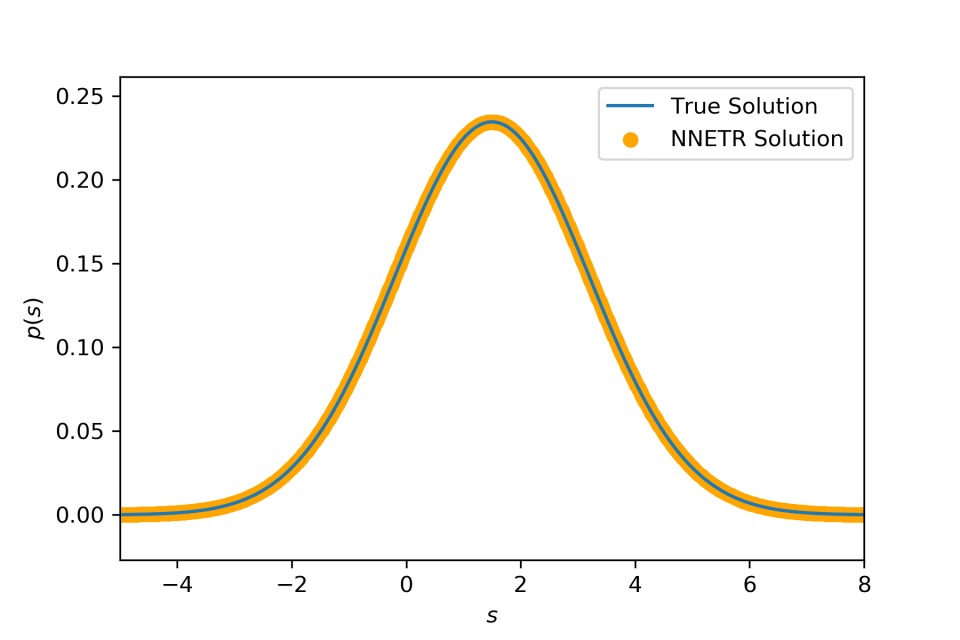
• Compounding a Gaussian distribution with mean distributed according to another Gaussian distribution yields (again) a Gaussian distribution $f(x)=\mathcal{N}(a,b^2+\sigma^2)$. $k(x\vert\mu)=\mathcal{N}(\mu,\sigma^2)$ and $p(\mu)=\mathcal{N}(a,b^2)$

• Compounding an exponential distribution with its rate parameter distributed according to a mixture distribution of two gamma distributions. Similar to the first example, we use $k(x,\theta)=\theta e^{-\theta x}$. But here we use $p(\theta)=q p(\theta\vert a_1)+(1-q)p(\theta\vert a_2)$ where $q$, $a_1$ and $a_2$ are parameters. It is clear that $p(\theta)$ is a mixture between two different gamma distributions such as it is a bimodal distribution. Following the first example, we have $f(x)=qf(x\vert a_1)+(1-q)f(x\vert a_2)$ where $f(x\vert a)=a(x+1)^{-(a+1)}$.

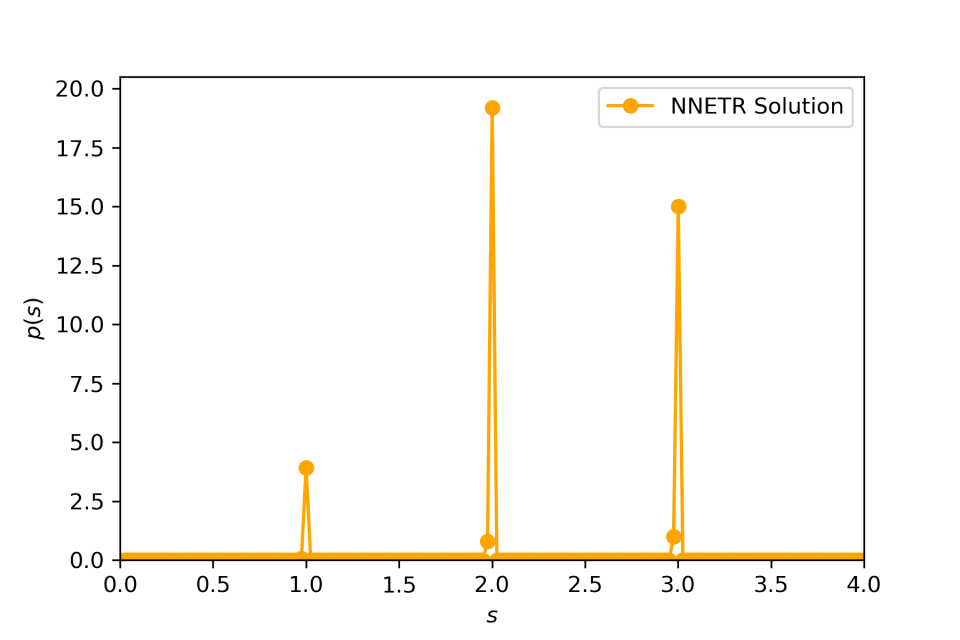
• Compounding an exponential distribution with its rate parameter distributed as a discrete distribution.